El Centro de Modelamiento Matemático (CMM) de la Facultad de Ciencias Físicas y Matemáticas (FCFM) de la Universidad de Chile y el Instituto francés de investigación en ciencias y tecnologías digitales (INRIA) realizaron el martes 9 de diciembre la segunda versión del Workshop PANDA, instancia que convocó a destacados investigadores e investigadoras en ecuaciones diferenciales parciales dispersivas, análisis no lineal y simulación numérica.
La actividad, se enmarca en el equipo asociado PANDA (Partial differential equations, Dispersive models and Nonlinear Analysis), un proyecto colaborativo entre instituciones chilenas y francesas dedicado al estudio de sistemas de ecuaciones dispersivas y sus aplicaciones, especialmente en la modelación de la propagación de ondas en la superficie del océano.
Durante esta nueva edición del workshop, expertos vinculados al proyecto expusieron los desarrollos más recientes en análisis no lineal y modelos matemáticos complejos. La actividad buscó fortalecer el intercambio académico, presentar resultados obtenidos en el marco de la colaboración internacional y fomentar nuevas líneas de trabajo. Para los organizadores, reunir a la comunidad científica representa una oportunidad estratégica para consolidar vínculos y promover investigación de frontera en matemáticas aplicadas.
En ese sentido Ricardo Freire, investigador posdoctoral de la Universidad de Chile, destacó que “este workshop es una instancia clave para el desarrollo del proyecto PANDA, porque nos permite reunir en un mismo espacio a investigadores de alto nivel que están impulsando avances en ecuaciones dispersivas y análisis no lineal. Estos encuentros fortalecen la colaboración entre Chile y Francia, consolidan redes de trabajo y nos permiten proyectar nuevas líneas de investigación que mantengan al CMM en la frontera del conocimiento matemático”.
María Eugenia Martínez, investigadora asociada al CMM, explicó que “el objetivo central del proyecto ha sido hacer riguroso desde el punto de vista matemático el comportamiento de los fluidos. Aunque muchos fenómenos pueden observarse experimentalmente o describirse desde la física, aún existen procesos que no están completamente entendidos ni por la física ni por la matemática. Por eso es tan relevante que las distintas disciplinas: matemática, física, biología y ecología, avancen de manera articulada”.
Agregó que “nuestro propósito es aportar una base matemática sólida a comportamientos que ya se conocen empíricamente, pero que aún carecen de una formulación rigurosa. En esa línea, los resultados obtenidos se concentran en dos avances principales: por un lado, el estudio teórico del comportamiento e interacción de ondas de agua con variaciones en el fondo en fluidos de poca profundidad; y por otro, el análisis numérico de cómo una onda interactúa con el fondo”.
Ecuaciones, modelos y simulaciones avanzadas
El académico Rafael Granero-Belinchón de la Universidad de Cantabria, abrió la jornada con una exposición sobre distintas ecuaciones diferenciales parciales que modelan ondas no lineales, destacando su carácter no local y los desafíos matemáticos asociados.
Posteriormente, el Prof. Raimund Bürger, investigador principal del CMM y académico de la Universidad de Concepción, presentó un modelo multilayer para estudiar la interacción entre tsunamis y bosques costeros, construido a partir de aproximaciones no hidrostáticas y validado con datos experimentales y de terreno. El trabajo es desarrollado junto a investigadores de España y Chile.
Conexión especial: Ceremonia del premio Ramanujan 2025
Durante la jornada, los participantes del workshop también se conectaron para seguir en vivo la 2025 Ramanujan Prize Ceremony, donde el galardón fue otorgado al Prof. Claudio Muñoz, investigador principal del CMM y miembro del comité organizador del workshop. El premio reconoce sus contribuciones fundamentales a las ecuaciones diferenciales parciales dispersivas y al estudio del comportamiento asintótico de soluciones en física matemática.
La comunidad del workshop siguió la ceremonia celebrada en la Budinich Lecture Hall, donde Muñoz ofreció la charla “The asymptotic stability of kinks in scalar field models”. Su reconocimiento internacional otorgó un carácter especial a esta edición del PANDA, subrayando el impacto global del trabajo que se desarrolla desde Chile en el área de las matemáticas aplicadas.
Por su parte el Prof. Muñoz, agradeció la instancia “haber recibido este reconocimiento en paralelo al desarrollo del workshop PANDA tiene un valor especial. Es un recordatorio de que el trabajo que hacemos, desde Chile y en colaboración internacional, está contribuyendo de manera significativa al avance de las ecuaciones dispersivas y al entendimiento de modelos fundamentales en física matemática. Saber que los investigadores e investigadoras de PANDA siguieron la ceremonia fue profundamente significativo y reafirma la importancia de seguir impulsando la investigación de frontera”.
Conocimiento matemático para responder a interrogantes
En la sesión de la tarde, el investigador André de Laire de la Université de Lille e INRIA abordó la existencia de ondas viajeras minimizantes para la ecuación de Gross–Pitaevskii en una geometría de canal bidimensional, destacando bifurcaciones críticas que separan soluciones unidimensionales de solitones verdaderamente bidimensionales. La presentación se basa en investigaciones conjuntas con Didier Smets y Philippe Gravejat.
El investigador André de Laire comentó que “este proyecto fue diseñado para tres años y finalizará en 2026. Luego buscaremos ampliar su alcance postulando a nuevas iniciativas, por ejemplo, a un proyecto internacional del CNRS, considerando que el CMM es un IRL perteneciente al CNRS. Esto podría darnos una mayor estabilidad a largo plazo, permitiéndonos continuar la colaboración y mantener, por muchos más años, el intercambio de estudiantes de doctorado y postdoctorado entre Francia y Chile”.
Nuevas aproximaciones numéricas y estabilidad de solitones
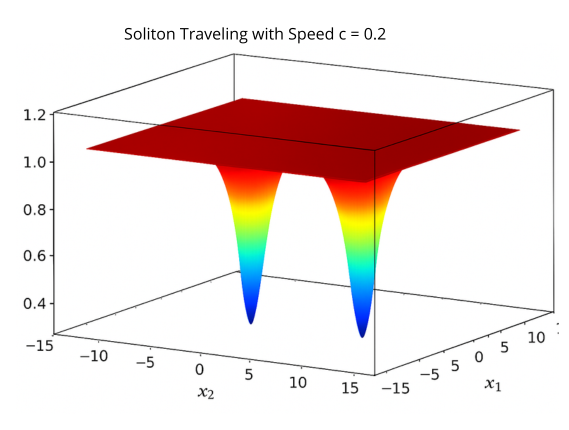
La programación continúo con la exposición de Sebastián Tapia-Mandiola (Université de Lille e Inria), quien presentó simulaciones numéricas de una ecuación de Schrödinger cuasilineal con condiciones de borde variables, enfocándose en la estabilidad de solitones, fenómenos de blow-up y la construcción de esquemas numéricos que preservan la energía. La jornada incluye además una charla dedicada a la estabilidad no lineal de solitones no singulares del modelo Principal Chiral Field en 1+1 dimensiones, una investigación que utiliza métodos de campos vectoriales aplicados previamente en ecuaciones de Einstein bajo el formalismo de Belinski–Zakharov.
El comité organizador del workshop está compuesto por los investigadores André de Laire, Claudio Muñoz y Ricardo Freire, y cuenta con el financiamiento del Programa Basal de ANID (FB210005) a través del CMM, además del respaldo de proyectos de investigación de Inria. La iniciativa reafirma el compromiso de ambas instituciones con el desarrollo de investigación avanzada en matemáticas aplicadas y con la formación de redes científicas que potencien el trabajo interdisciplinario.
PANDA (PArtial differeNtial equations, Dispersive models and nonlinear Analysis) es una equipo Inria-CMM que busca establecer lazos colaborativos entre equipos chilenos y franceses, en matemáticas aplicadas. El objetivo principal es el estudio de sistemas de ecuaciones en derivadas parciales basado en el análisis no lineal y las simulaciones numéricas. La principal aplicación es al modelamiento de la propagación de olas en la superficie del océano ante condiciones realistas.
Revisa las publicaciones recientes:
- Decay of small energy solutions in the ABCD Boussinesq model under the influence of an uneven bottom. C. Maulén, C. Muñoz y F. Poblete, (2025) https://arxiv.org/abs/2507.0648
En este trabajo se sientan las bases de la descripción en tiempos grandes de las soluciones perturbadas de modelos de fluidos a fondo variable, en las cercanías del estado de reposo.
- Dynamics of generalized abcd Boussinesq solitary waves under a slowly variable bottom. A. de Laire, O. Goubet, M. E. Martínez, C. Muñoz y F. Poblete, (2025) https://hal.science/hal-05379838
En este trabajo trabajamos la dinámica de una onda solitaria de tipo abcd que modela aguas poco profundas, que se mueve en la influencia de un fondo variable. Se muestra por primera vez y de forma rigurosa la supervivencia de la ola si el fondo tiene una variación lenta en espacio y tiempo.
Esta actividad contó con el financiamiento del Proyecto Basal ANID FB210005.
Posted on Dec 12, 2025 in Noticias en castellano




 Noticias en español
Noticias en español